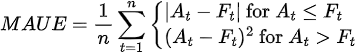NOTE: Only some of these Error Metrics can be used as evaluation metrics. The rest are computed metrics (not used for evaluating which model is better than another).
Mean Absolute Error (MAE)
An error measurement between paired observations expressing the same phenomenon. Examples of Y versus X include predicted versus observed comparisons, subsequent time versus initial time, and one measurement technique versus an alternative measurement technique.
Formula:

Interpretation: Lower is better.
Benefits:
-
Easily interpretable.
-
No favoritism towards over- or under-predictions.
Shortcomings:
-
Relative size of the error is not obvious as with percentages.
Mean Absolute Percent Error (MAPE)
A prediction accuracy measurement of a forecasting method. Also known as mean absolute percentage deviation.
Formula:

Interpretation: Lower is better.
Benefits:
-
Easily explainable.
-
Scale-independent / expressed as a percentage.
Shortcomings:
-
Returns undefined values when forecasting for actual values of zero.
-
Favors models that under-forecast due to heavier penalty on forecasts higher than actuals. Forecasts below actuals cannot be worse than 100% Mean Absolute Percent Error (MAPE).
Mean Absolute Scaled Error (MASE)
A measure that determines how effective forecasts generated through an algorithm are by comparing the forecast predictions with the output of a naïve forecasting approach.
Formula:
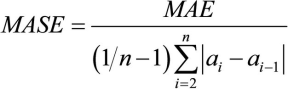
Interpretation: Lower is better
Benefit: Independent of the data's scale, so it can be used to compare forecasts across data sets with different scales.
Mean Asymmetric Over Error (MAOE)
A combination of both Mean Squared Error (MSE) and Mean Absolute Error (MAE) depending on whether the predicted value is over or under the actual value. If the predicted value is over the actual value, then the error metric applied is MSE (squared difference). If the predicted value is under the actual value, then the error metric applied is MAE (absolute difference).
Formula:
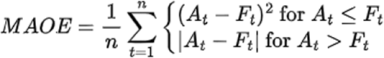
Interpretation: Lower is better.
Benefit: Favors models that under predict. May be useful if there is a difference in penalty in real world application for over predictions.
Shortcomings: Can over penalize a model for over predicting just once or twice way more than under predicting consistently.
Mean Asymmetric Under Error (MAUE)
Similar to Mean Asymmetric Over Error (MAOE), but applies Mean Squared Error (MSE) to predictions below the actual value and Mean Absolute Error (MAE) to predictions above the actual value.
Formula:
Interpretation: Lower is better.
Benefit: Favors models that over predict. May be useful if there is a penalty differences in real world application for under predictions.
Shortcomings: Can over penalize a model for under predicting just once or twice way more than over predicting consistently.
Mean Bias Error (MBE)
Mean Bias Error (MBE) is primarily used to estimate the average bias in a model and determine what is needed to correct the model bias. MBE captures the average bias in the prediction.
Formula:
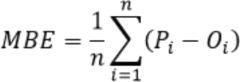
Interpretation: Typically not used as a measure of model error, as high individual errors in prediction can also produce a low MBE. MBE reflects a prediction's average bias. A positive value represents overestimating bias and a negative value represents an underestimating bias.
Shortcomings: This is typically not used to measure model error.
Mean Percent Error (MPE)
The computed average of percentage errors by which a model's forecasts differ from actual values of the forecasted quantity.
Formula:
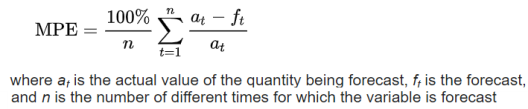
Interpretation: Closer to zero is better.
Benefits: Can be used as a measure of the bias in the forecasts
Shortcomings:
-
Measure is undefined when a single actual value is zero.
-
Positive and negative forecast errors can offset each other.
Mean Squared Error (MSE)
The average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.

Interpretation: Lower is better.
Benefits:
-
Increased penalty for larger errors.
-
Ensures positives values for easy interpretation.
Shortcomings:
-
Less intuitive than MAE.
Mean Squared Logarithmic Error (MSLE)
A measure of the ratio between the true and predicted values. MSLE is a variation of Mean Squared Error (MSE).
Formula:
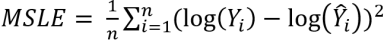
Interpretation: The loss is the mean over the seen data of the squared differences between the log-transformed true and predicted values.
Benefit: Treats small differences between small true and predicted values approximately the same as large differences between large true and predicted values.
Shortcomings: Penalizes underestimates more than overestimates.
Median Absolute Error (MedAE)
The loss is calculated by taking the median of all absolute differences between the target and the prediction. If ŷ is the predicted value of the sample and y1 is the corresponding true value, then the median absolute error estimated over n samples is defined as follows:
Formula:
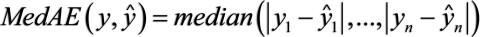
Interpretation: Lower is better
Benefit: Robust to outliers
Symmetric Mean Absolute Percent Error (SMAPE)
An accuracy measure based on percentage (or relative) errors.
Formula:
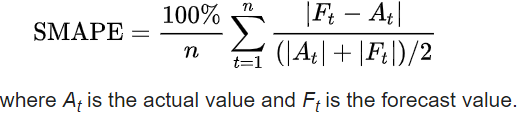
The absolute difference between At and Ft is divided by half the sum of absolute values of the actual value At and the forecast value Ft. The value of this calculation is summed for every fitted point t and divided again by the number of fitted points n.
Interpretation: Lower is better
Benefits:
-
Expressed as a percentage.
-
Lower and upper bounds (0% - 200%).
Shortcomings:
-
Unstable when both the true value and the forecast value are close to zero.
-
Not as intuitive as MAPE (Mean Absolute Percent Error).
-
Can return a negative value.
R2 (R-Squared)
A statistical measure of fit that indicates how much variation of a dependent variable is explained by the independent variables in a regression model.
Formula:

Interpretation: Higher is usually better; Measures the strength of the relationship between independent and dependent variables in a regression model; Ranges between 0 (No Correlation 0 and 1 (Perfect Correlation)
Benefits: Commonly used as a measurement technique
Shortcomings:
-
Sometimes, a high R-Squared value can indicate problems with the regression model.
-
Does not reveal the causation relationship between the independent and dependent variables.
Symmetric Mean Absolute Percent Error (SMAPE)
A measure to compare true observed response with predicted response in regression tasks.
Formula:
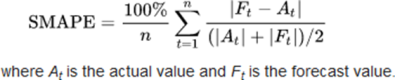
Interpretation: The value of this calculation is summed for every fitted point t and divided again by the number of fitted points n.
Benefits: Has both a lower bound and an upper bound.
Shortcomings: If the actual value or forecast value is 0, the value of error goes to the error upper limit.