Appendix 4: Interpretability

Feature Effects

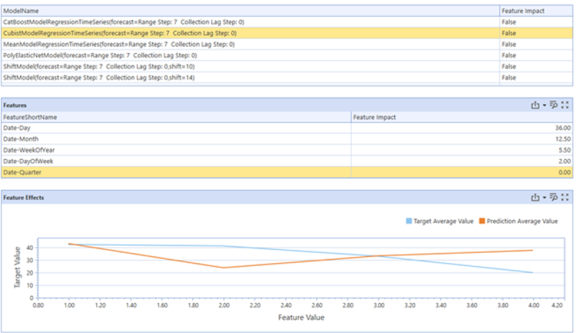
For a specific trained model, a specific feature of that model and its value, the feature effects shows the average prediction of that model versus the average value of the actuals, The average is taken across all dates where that feature was equal to the specific feature value. Use this information to see how accurate a model is on average for a specific feature. Used with the feature impact score of the feature, this is a useful diagnostic for decomposing the model performance and identifying potential areas for improvement. This could mean adding different impactful features so a model is less reliant on a feature that shows large deviances between average predictions and average actuals, or removing a poorly performing feature.

Take for example, given model A, a daily data set between 1/1/2020 and 1/1/2021, binary feature B that takes on values 0 and 1 and is used by model A:

• The feature effects graph for feature B would have on the X axis 0 and 1.

• The Y axis over 0 would be the average value of the actuals on all days the feature took on 0, as well as the average prediction on all days the feature took on value 0. The same applies for a feature value of 1.

The following example looks at the feature effects of the Cubist Model for the feature Date-Quarter and a specific target. The average prediction on all the days the Date-Quarter takes on a value of 2 is roughly 20, and the average actuals is roughly 40. This same logic can be applied to all the feature values Date-Quarter takes on, namely, 1, 2, 3, and 4.

Feature Impact

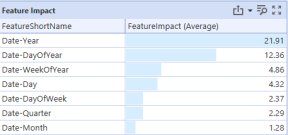
Feature impact is a way to understand the overall importance a feature has to a model’s predictions. The higher a feature's impact score, the more significant that feature is to the model’s outputs.

For example, the following chart shows the Date-Year feature has the most significant impact on the model’s predictions, where Date-Month was rather trivial in comparison. Specifically, changes in the Date-Year feature cause large changes in the model’s output, whereas changes in the Date-Month feature cause much smaller changes in the model output.

There are various and evolving mathematical methods for calculating feature's impact on a model. The two methods implemented by the engine are Permutation Importance and Shapley Additive Explanations (SHAP).

The permutation importance of a feature is the decrease in the model’s prediction quality when that feature is randomly shuffled. This removes the model’s ability to use that feature, but not its reliance since the model is already trained on the unshuffled version of the feature. The performance decrease's magnitude is the feature's relative importance for the model. If shuffling the feature has little effect on the model's error, that feature is not important since the model did not rely heavily on the feature. If shuffling a feature causes a large performance decrease, the model relies heavily on that feature, meaning the feature is important.

The SHAP feature impact value indicates the average magnitude this feature moved the model’s prediction from the model's average prediction across all data points. SHAP is an algorithm for calculating Shapley values, where the Shapley values are the feature's fair attribution contributions to the model output for a specific data point.

If a model’s average prediction across all data points is x, the Shapley values of the features for a specific data point x’ tells how the model got from its average prediction x to the specific prediction for x’, where x’=x+sum(Shapley values) and the sum is taken across all features the model uses. The average magnitude of a specific feature's Shapley value for across all data points predicted can go from specific data point explanations to an overall feature impact.

For more information on the specific math behind the SHAP implementation, see: https://christophm.github.io/interpretable-ml-book/shap.html

Prediction Explanations

For a specific predicted data pot, prediction explanations show how the model uses the features to form that prediction. XperiFlow uses Shapley Additive Explanations (SHAP) as its prediction explanation method. SHAP for prediction explanations and for feature impact is the same algorithm. The only difference in in prediction explanations, the Shapley magnitude average values of the Shapley are not taken. Instead, the Shapley values at each data point are shown to explain how the model got from its average prediction to the actual prediction.

This can be seen in the following graphic. Zooming in on the first predicted point, the model’s prediction is higher than average, and the Shapley values represent this. The orange boxes show positive Shapley values, driving the prediction upward from the average. The blue boxes show negative Shapley values, driving the prediction downwards. For the first data point, the positive Shapley values far outweigh the negative Shapley values, leading to a higher prediction. Each box is associated with a specific feature, and shows for the feature and data point how the feature affects the prediction output; either by driving it down, driving it up, or being insignificant. The sum of the Shapley values plus the average model prediction gives the model prediction for a specific data point.

Prediction Intervals

A prediction interval is a value range for a data point prediction that likely contains the true actual future value of the data point. Prediction intervals are useful since time series data is a stochastic process, which means an underlying process generates the actual data has randomness involved. The prediction interval can help account for this randomness.

Prediction intervals instantiate using an alpha value. For example, an alpha of .05 gives a 95% prediction interval. This means if the stochastic process generating the data is sampled an infinite number of times, you could expect 95% of the actual values to fall within this interval. These intervals move the models from simply predicting a point forecast, which can be interpreted as the mean of all the potential futures, to forecasting the distribution of the potential futures.

In the following example, the orange line is the point forecast and the shaded blue region around the orange line is the prediction interval.

There are various and evolving methods to calculate prediction intervals. The XperiFlow engine uses conformal prediction intervals, parametric prediction intervals, and non-parametric prediction intervals.

Parametric prediction intervals assume the error of the data follows a specific distribution (where the error is the difference between the actual value and the predicted value). The error metrics statistics are used to fit this distribution. Then, depending on the alpha level that instantiates the prediction interval, the proper values can be extracted from the distribution to surround the point forecast and form the prediction interval.

The non-parametric approach works similarly without assuming the error metrics. The non-parametric approach orders errors by size and uses the (1-alpha)% error as the top of the interval, and the (alpha)% error as the bottom. Specifically, if alpha is .05, the 95% percent largest error forms the top of the interval, and the 95% smallest error (which is either negative or zero) forms the bottom of the interval.